Движитель искажения пространства: сверхбыстрое перемещение в пределах Общей Теории Относительности

Изучая Специальную Теорию Относительности, мы узнаем, что ничто не может двигаться быстрее, чем скорость света в вакууме. Этот факт остается верным и в Общей Теории Относительности, хотя нужно сделать одно уточнение: в Общей Теории Относительности ничто не может двигаться быстрее света в местной системе отчета.

Исходя из нашего повседневного опыта, основанного на Евклидовом пространстве, будет естественным предположить, что если в местной системе отчета нельзя превысить скорость света, тогда если даны две точки, расположенные на расстоянии D друг от друга, то невозможно совершить путешествие из одной точки в другую и обратно за время меньшее, чем 2D/c (где с - скорость света). Конечно, из теории относительности, мы знаем, что личное время путешественника может быть сколько угодно малым, в зависимости от того, насколько близко к скорости света он путешествует. Но факт состоит в том, что при соблюдении Общей Теории Относительности, мы можем без привлечения нестандартной топологии (червоточин и т.п.) совершить путешествие туда и обратно в максимально короткий срок не только по времени путешественника, но и по времени наблюдателя.

Здесь я приведу простой пример, как это можно осуществить. Основную идею легко понять, если представить ранние часы нашей расширяющейся Вселенной и двух наблюдателей в ее разных частях, которые непрерывно удаляются друг от друга с громадной скоростью. Легко убедиться, что если мы определяем скорость расширения, как норму изменения расстояния в местной системе отчета по местному времени, то мы получим скорость намного большую скорости света. Это не означает, что наши наблюдатели будут путешествовать быстрее света, они всегда будут двигаться в своих локальных световых конусах. Огромная скорость удаления друг от друга возникает непосредственно от расширения пространства-времени.

Предыдущий пример показывает как можно использовать расширение пространства-времени для удаления от какого-либо объекта. Таким же самым способом можно использовать сокращение пространства-времени для приближения к какому-либо объекту на произвольно большой скорости. Это основа для сверхбыстрого перемещения, которое я хочу предложить: нужно создать локальную деформацию пространства-времени, которая произведет расширение пространства-времени позади корабля и сжатие пространства-времени перед ним. Таким образом космический корабль будет удаляться от Земли и непосредственно приближаться к отдаленной звезде. Аналогично нужно инвертировать процесс, чтобы вернуться обратно.

Ну и сейчас я представлю математическое обоснование вышеизложенного процесса. Я сделаю это, пользуясь представлением 3+1 пространства [1], [2] в Общей Теории Относительности, так как это позволит чисто интерпретировать результаты. В этом представлении пространство-время описано как разложение пространственных гиперповерхностей по постоянной координате времени t. Геометрия пространства-времени при этом дается в терминах следующих величин: 3-мерная γ_ij гиперповерхности, функция отклонения α , дающая интервал собственного времени между ближайшими гиперповерхностями, измеренный "Эйлеровыми" наблюдателями (т.е. наблюдателями, чья 4-мерная скорость является нормалью к гиперповерхности), и вектор смещения βⁱ связывающий пространственные координатные системы на различных гиперповерхностях. Используя эти величины метрику пространства-времени можно записать так:

ds2 = -dτ2 = gαβ dxα dxβ
                                     = -(α2 - βiβi) dt2 + 2βidxidt + γijdxidxj.      ()

Обратите внимание, что на всем протяжении метрики, где γ_ij положительно определена для всех значений t пространство-время гарантировано будет глобально гиперболическим. Поэтому любое пространство-время описанное в представлении 3+1 не будет иметь никаких замкнутых причинных кривых. Предположим теперь, что наш корабль движется вдоль оси х декартовой системы координат. Мы хотим найти функцию, которая протолкнет наш корабль по траектории описанной произвольной функцией времени xs(t). Функция, имеющая это свойство выводится из (G = c = 1) :

α = 1 ,                        ()
βx = - υs(t)ƒ(rs(t)),      ()
βy = βz = 0,                ()
γij = δij,                       ()

где:

υs(t) = dxs(t)/dt,             rs(t) = [ (x - xs(t))² + y² + z² ]½,

и где ƒ это функция:

             (6)

с произвольными параметрами R>0 и σ >0 . Обратите внимание, что для больших значений σ функция приближается к быстрым цилиндрическо-подобным функциям:

             (7)

С вышеупомянутыми определениями мы можем переписать метрику (1):

ds2 = - dt2 + (dx - υsƒ(rs)dt)2 + dy2 + dz2.       ()

Геометрию нашего пространства-времени легко понять из предыдущих уравнений.

Сначала, из уравнения (5), мы видим, что 3-мерная геометрия гиперповерхностей всегда плоская. Кроме этого факт того, что отклонение α=1, говорит что времeниподобные кривые являются нормалью к гиперповерхностям, то есть, "Эйлеровы" наблюдатели находятся в свободном падении. Впрочем, пространство-время не совсем плоско из-за присутствия неравномерного сдвига. Однако, так как сдвиг вектора обращается в ноль для r_s>>0, мы видим, что в любой момент времени t пространство-время будет чрезвычайно плоским всюду , кроме области с радиусом порядка R с центром в точке (x_s(t), 0, 0).

Так-как 3-мерная геометрия гиперповерхностей плоская, информация о кривизне пространства-времени будет содержаться во внешнем тензоре кривизны К_ij. Этот тензор описывает, как 3-мерные гиперповерхности включены в 4-мерное пространство-время, и определен как:

           (9)

где D_i обозначает ковариантное дифференцирование относительно 3-мерной γ_ij. Из определения α и γ_ij нетрудно увидеть, что формула сводится к:

Kij = 0,5 (∂iβj + ∂jβi)      (10)

Расширение θ объема пространства, связанного с "Эйлеровыми" наблюдателями, в терминах К_ij выглядит как:

θ = - α Tr K .      (11) 

Откуда легко показать, что:

.      (12)

Рисунок (1) показывает график функции θ от x и ρ = (y² + z²)^1/2, в частном случае, когда ρ = 8 и R = υ_s = 1. Центр возмущения соответствует положению космического корабля x_s(t). Мы можем ясно увидеть как объем пространства расширяется перед кораблем и сжимается позади него.

Рисунок 1

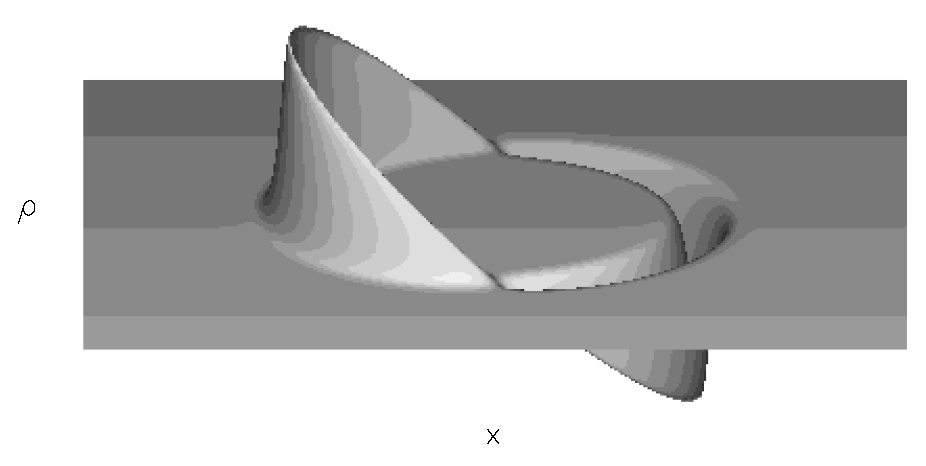
Чтобы доказать, что траектория корабля действительно является времениподобной кривой, независимо от значений υ_s(t), мы заменяем x = x_s(t) в метрике (8). . Так легко увидеть, что для траектории космического корабля мы будем иметь:

dτ = dt .      (13)

Это подразумевает не только то, что космический корабль двигается по времениподобной кривой, но также и что его время собственное эквивалентно времени координатной системы. Так как время системы координат также равно времени собственному отдаленных наблюдателей в некоторой плоскости, мы заключаем, что космический корабль не подвергается никакому замедлению времени, покуда он перемещается. Также просто доказать, что космический корабль двигается по геодезической прямой. Это означает также, что даже при том, что ускорение в координатной системе может быть произвольной функцией времени, соответствующее ускорение вдоль траектории космического корабля всегда будет нолем. Кроме того, не трудно убедиться, что когда параметр σ является большим, деформирующие силы в непосредственной близости космического корабля являются очень небольшими (при условии, что R является большим чем размер космического корабля). Конечно, в области, где r_s R деформирующие силы могут быть действительно очень большими .

Чтобы увидеть, как можно использовать эту метрику, чтобы совершить путешествие туда и обратно к отдаленной звезде в произвольно небольшой интервал времени, позвольте нам рассмотреть следующую ситуацию: Две звезды A и B разделены интервалом D в плоском пространстве-времени. Во время t₀, космический корабль начинает удаляться от нее на скорости υ < 1 используя ракетные двигатели. Когда космический корабль остановится на расстоянии d от A, предположим, что d:

R << d << D .      (14)

Именно в этой точке возмущение пространства-времени вневписанного типа, по центру от положения космического корабля, появляется впервые. Это возмущение таково, что корабль оказывается отодвинутым от точки A с ускорением относительно системы координат, которое внезапно превратилось из 0 в константное значение α. Так как корабль изначально находился в покое (υ_s = 0) возмущение будет гладко развиваться из плоского пространства-времени (см. формулу 8).

Когда корабль будет на половине пути между A и B возмущение изменится таким образом, что ускорение внезапно поменяется с α на - α . Если ускорение во второй половине пути будет противоположно тому, что мы имели в первой половине, то космический корабль в конечном счете окажется в покое на расстоянии d от B в этот момент возмущение пространства-времени исчезнет ( снова υ_s=0 ). Полет таким образом завершен, корабль снова перемещается в пространстве со скоростью υ.

Если изменение направления ускорения будет очень быстрым, то время путешествия в системе координат наблюдателя будет по сути равняться:

.      ()

Так как обе звезды остаются в плоском пространстве, их время собственное равно времени системы координат. Собственное время, прошедшее на космическом корабле будет:

.      (16)

c γ = (1 - υ²)^-1/2. Мы видим, что замедление времени присутствует только в начальной и конечной стадии пути, когда корабль движется сквозь обычное плоское пространство-время. Теперь, если будет соблюдаться условие (14), мы будем иметь:

.      (17)

Теперь ясно видно, что Т может быть насколько угодно маленьким, в зависимости от значения α. Так как путешествие туда и обратно к звезде будет всего лишь в два раза дольше, мы можем заключить ,что корабль может вернуться назад к звезде A за произвольно маленький промежуток времени как с точки зрения экипажа, так и сточки зрения звезды. Скорость корабля при этом будет намного быстрее скорости света. Однако, как мы уже говорили, корабль будет оставаться на времениподобной траектории, то есть в своем локальном световом конусе: луч света тоже будет перемещен искажением пространства-времени. Механизм двигателя, основанного на локальном искажении пространства сам напрашивается на знакомое название из научной фантастики: "двигатель искажения пространства" (warp drive).

Метрика, только-что описанная мною, имеет впрочем один важный недостаток: она нарушает все три энергетических условия (слабое, энергодоминантное и сильное [3]). Оба - и слабое, и энергодоминантное энергетических условия требуют, чтобы энергетическая плотность была положительной для всех наблюдателей. Если Вы вычисляете Эйнштейновский тензор из метрики (8) и используете тот факт, что 4-мерные скорости "Эйлеровых" наблюдателей дают:

nα = (1/α)(1,-βi) ,    nα = (-α,0) ,      ()

Откуда можно показать, что эти наблюдатели будут видеть энергетическую плотность:

.     (19)

Факт, что это выражение всюду является отрицательным, означает, что слабое и энергодоминантное условия нарушены. Подобным способом можно показать, что сильное энергетическое условие тоже нарушено.

Отсюда мы видим, что так же, как в случае с червоточинами, мы нуждаемся в экзотическом веществе, чтобы путешествовать быстрее скорости света. Однако, даже если Вы полагаете, что экзотическое вещество запрещено классическими законами, известно, что квантовая теория поля разрешает существование областей с рассеивающими энергетическими плотностями при некоторых специальных обстоятельствах (как, например, при эффекте Casimir [4]). Потребность в экзотическом веществе поэтому не обязательно отбрасывает возможность использования искажения пространство-времени так, как описано выше, для сверхбыстрого межзвездного перемещения.

В заключение, хочу добавить, что даже при том, что пространство-время, описанное метрикой (8) является глобально-гиперболическим, и следовательно не содержит никаких закрытых причинных кривых, вероятно не очень трудно создать пространство-время, которое действительно содержит такие кривые, используя идею подобную той, что представлена здесь.

Автор хочет поблагодарить Bernard F. Schutz и Gareth S. Jones за множество полезных комментариев.

Сылки

[1] C.W. Misner, K.S. Thorne and J.A. Wheeler, Gravitation, W.H. Freeman, 1973.

[2] J.W. York, “Kinematics and Dynamics of General Relativity” in: Sources of Gravitational Radiation, ed. L.L. Smarr, pp. 83-126, Cambridge University Press, 1979.

[3] S.W. Hawking and G.F.R. Ellis, The Large Scale Structure of Spacetime, Cambridge University Press, 1973.

[4] B.S. DeWitt, in General Relativity: An Einstein Centenary Survey, edited by S.W. Hawking and W. Israel, Cambridge University Press, Cambridge, 1979.

Другие публикации по этой теме

• Francisco S. N. Lobo, Phantom energy traversable wormholes (2005)
• Francisco S. N. Lobo and Matt Visser, Fundamental limitations on "warp drive" spacetimes (2004)
• M. Tajmar, O. Bertolami, Hypothecial Gravity Control and Possible Influence on Space Propulsion (2004)
• Thomas A. Roman, Some Thoughts on Energy Conditions and Wormholes (2004)
• S. Krasnikov, Counter example to a quantum inequality (2004)
• Francisco S. N. Lobo, Surface stresses on a thin shell surrounding a traversable wormhole (2004)
• Uwe R. Fischer and Matt Visser, Warped space-time for phonons moving in a perfect nonrelativistic fluid (2003)
• Francisco Lobo and Paulo Crawford, Time, Closed Timelike Curves and Causality (2003)
• Leo Brewin, Classroom computer animations of relativistic objects (2003)
• Jose Natario, Warp Drive With Zero Expansion (2002)
• Francisco Lobo and Paulo Crawford, Weak energy condition violation and superluminal travel (2002)
• William A. Hiscock, From Wormholes to the Warp Drive: Using theoretical physics to place ultimate bounds on technology (2002)
• C.B. Hart, R. Held, P.K. Hoiland, S. Jenks, F. Loup, D. Martins, J. Nyman, J.P. Pertierra, P.A. Santos, M.A. Shore, R. Sims, M. Stabno, T.O.M. Teage, On the Problems of Hazardous Matter and Radiation at Faster than Light Speeds in the Warp Drive Space-Time (2002)
• O. Bertolami and M. Tajmar, Hypothetical Gravity Control and Implications for Spacecraft Propulsion (2002)
• F. Loup, R. Held, D. Waite, E. Halerewicz, Jr., M. Stabno, M. Kuntzman, R. Sims, A causally connected superluminal Warp Drive spacetime (2002)
• Michael J. Pfenning, L.H. Ford, The unphysical nature of "Warp Drive" (2001)
• F. Loup, D. Waite, E. Halerewicz Jr, Reduced Total Energy Requirements for a Modified Alcubierre Warp Drive Spacetime (2001)
• Pedro F. Gonzalez-Diaz, On the warp drive space-time (2000)
• Chris Van Den Broeck, On the (im)possibility of warp bubbles (2000)
• Chris Van Den Broeck, A `warp drive' with more reasonable total energy requirements (1999)
• Chad Clark, William A. Hiscock, and Shane L. Larson, Null geodesics in the Alcubierre warp drive spacetime: the view from the bridge (1999)
• Matt Visser , Bruce Bassett , Stefano Liberati, Superluminal censorship (1999)
• Bernhard Haisch and Alfonso Rueda, Toward an Interstellar Mission: Zeroing in on the Zero-Point-Field Inertia Resonance (1999)
• Robert J Low, Speed Limits in General Relativity (1998)
• Michael John Pfenning and L. H. Ford, Quantum Inequality Restrictions on Negative Energy Densities in Curved Spacetimes (1998)
• C.J. Fewster and S.P. Eveson, Bounds on negative energy densities in flat spacetime (1998)
• S. V. Krasnikov, Hyperfast Interstellar Travel in General Relativity (1998)
• Allen E. Everett and Thomas A. Roman, A Superluminal Subway: The Krasnikov Tube (1997)
• William A. Hiscock, Quantum effects in the Alcubierre warp drive spacetime (1997)
• Claes R Cramer, Photon propagation in a stationary warp drive space-time (1995)